Ératosthène de Cyrène (actuellement en Libye) est né vers 276 av.JC et décédé à Alexandrie vers 194 av.JC.

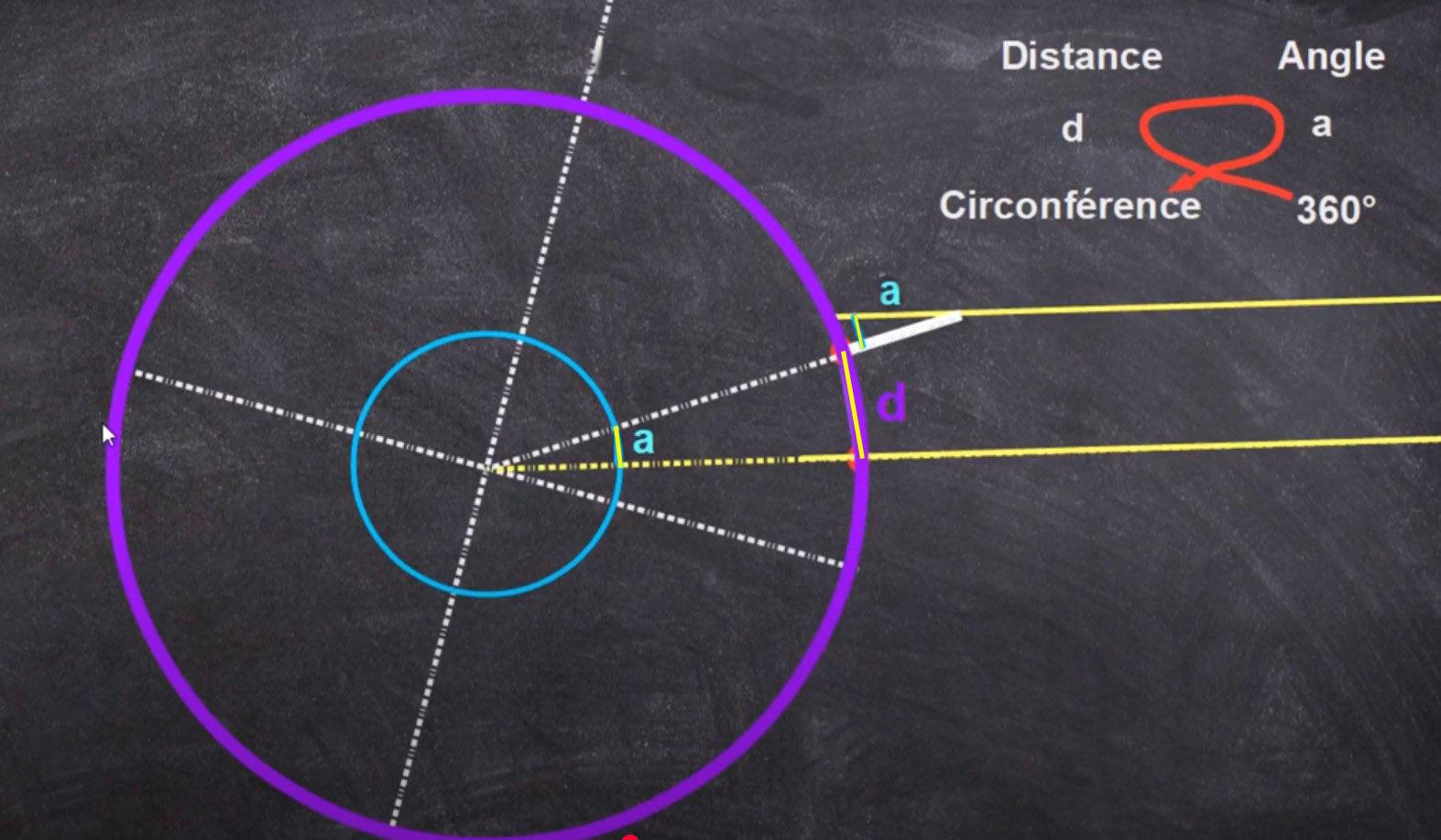
1) Diamètre et circonférence de la Terre
on admet que :
C = π x D ( C circonférence d'un cercle de diamètre D )
Alexandrie Syène sont à peu près sur un même méridien
Soleil si loin que ses rayons parallèles

… à Syène (actuelle Assouan), tropique du Cancer. Il remarque que le Soleil atteint le fond des puits le 21 juin,
jour du solstice d’été, il éclairait le fond des puits, donc qu’il était à la verticale, contrairement à Alexandrie.
( voir fig 1)

Différence de latitude entre Syène et Alexandrie, c’est la mesure de l’angle a=7°12’.
Ératosthène donne 1/50 de cercle (7°12’) pour la hauteur du Soleil au solstice.
Distance de Syène à Alexandrie : le pas du dromadaire, 100 stades par jour sur 50 jours. Donc 5000 stades.
Tour de la Terre est donc : 50x5000= 250000 stades.
si 1 stade = 157.5 m ?
alors 157.5x250000 = 39375 km… pas mal !
diamètre de la Terre 39375/3,14 = 12533km (en fait 12756 équateur et 12714 pôle).

Eratosthène aurait pu aussi ...

2) Diamètre de la Lune
Un jour d'éclipse partielle de Lune, évaluer le disque de l'ombre de la Terre sur la Lune en dessinant.
Entre 3 et 4 disques de la Lune dans celui de la Terre soit environ 3,5.
12533/3.5=3580 km (en fait 3474 km) … pas mal !
( il y a 2200 ans pour Aristarque la Lune sur le ciel parcourt son diamètre en 1h,
un jour d’éclipse total de Lune le cylindre d’ombre de la Terre parcourt toute la Lune en 2h,
donc le disque de la Terre est 3 fois (2+1) celui de la Lune)

3) Distance Terre Lune

a - Un jour de Soleil dans une pièce, persienne fermée, le Soleil rentre par une petite fente et
atteint le mur d'en face.
( voir fig 2 )

Le Soleil apparait parfaitement rond, c'est son image inversée.
Image 5cm de diamètre, distance à la persienne 5m environ.
Ce rapport distance diamètre est le même que celui distance au Soleil sur diamètre de Soleil.
( triangles homothétiques opposés par le sommet)
Donc 100 fois le diamètre du Soleil entre lui et nous.

b - Un jour d'éclipse total du Soleil, la Lune cache complètement le Soleil
Si on admet que les disques apparents du Soleil et de la Lune sont pratiquement égaux.
Donc remplaçons Soleil par Lune …
il y a donc 100 Lunes entre elle et nous.
Alors 3580x100 = 358000 km ( en fait, la distance moyenne entre la Terre et la Lune est d'environ 384 400 km.
( Cependant, cette distance peut varier entre 363 300 km et 405 500 km en raison de l'orbite elliptique de la Lune. )
Eratosthène aurait pu !

(pour le diamètre du Soleil et sa distance … voir Aristarque de Samos)

 

Aristarque de Samos (310-230 avJC)

Fut le premier à proposer un modèle héliocentrique de l'univers dans lequel le Soleil, et non la Terre, était au centre.
Aristarque de Samos avait aussi estimé que notre satellite se trouvait à 486 000 km de la Terre.

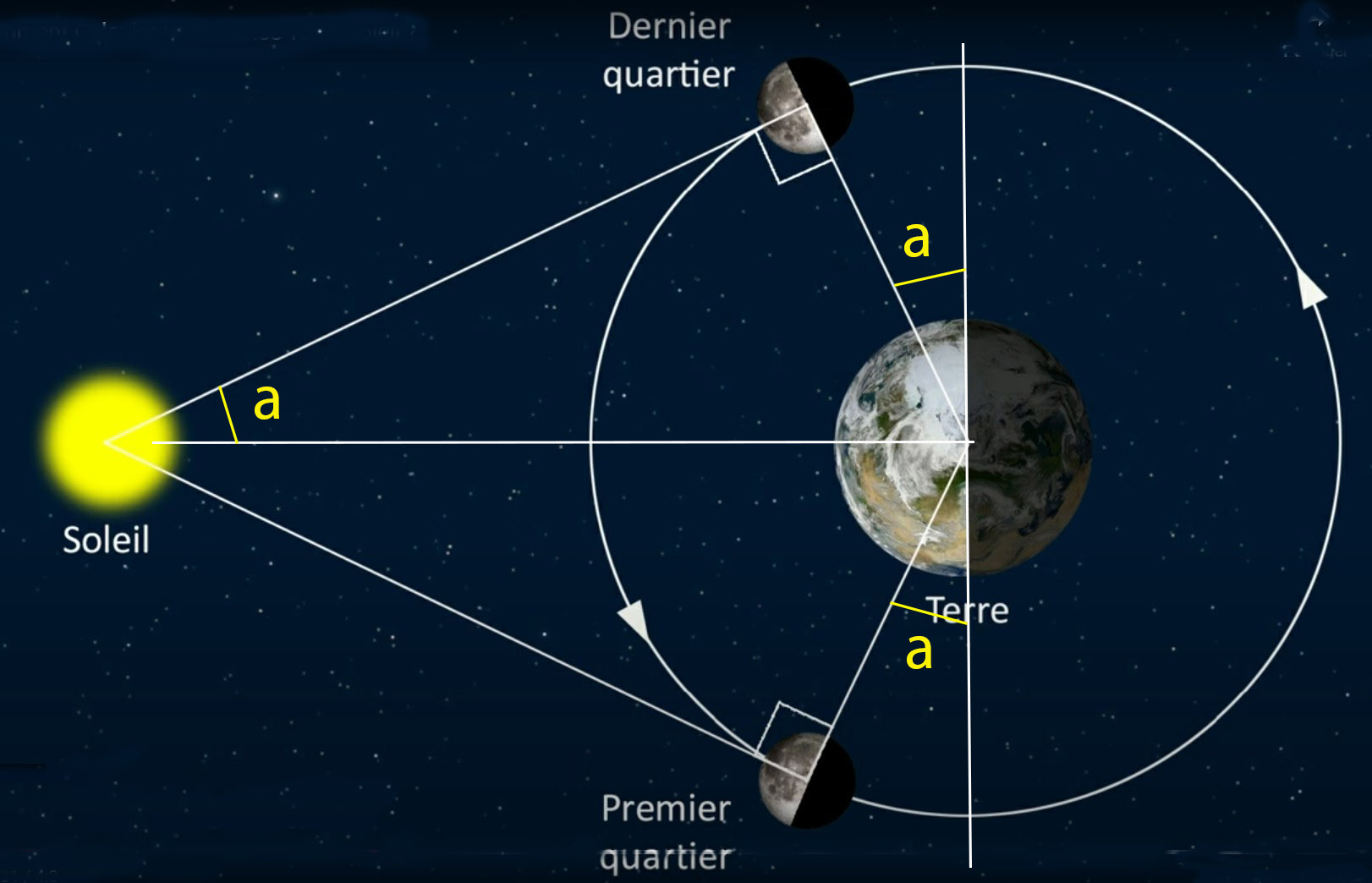
Méthode utilisée pour la distance Terre - Soleil:
Il remarque que le temps passé entre premier et dernier quartier est plus court que celui entre le dernier quartier et le premier.
(voir fig 3 )

Il l'estime la différence à 1 jour et en déduit que le Soleil est loin mais à distance finie.
( en réalité 1h 10 min mais difficile à évaluer ). et la lunaison 29 jours ( tour de la lune complet )
Alors du premier quartier au dernier 14j (en fait 14j 17h 25mn) et du dernier au premier 15j (en fait 14j 18h 35mn)
On a soit 360x(14/29)+2a = 180 , soit 360x(15/29)-2a = 180
Calcul de a donc a = 3,1°
sin a = TL/TS => TS = TL/sin a
( TL : distance Terre - Lune et TS : Terre - Soleil; le sin a se mesure sur un cercle de rayon 1 )
TS = 7.108.000 km
(en fait ~150.000.000 km et le diamètre dans le rapport 1/100)
Grosse imprécision due à la différence de 1j au lieu de 1h10 dans le temps évalué, mais bonne déduction.

( télécharger le pdf)